Biofysiske grænser for Vækst
Emil Urhammer & Inge Røpke
En af konsekvenserne af det biofysiske perspektiv på økonomien er fremhævelsen af grænser for vækst. I det biofysiske perspektiv er jorden et system, som primært får sin energi fra solen, og samfundsøkonomien ses som en metabolisk organisme, der udvikler sig inden for biosfærens begrænsede rammer. Jo større organismen bliver – baseret på stadig større gennemstrømning af energi og materialer – des større bliver risikoen for, at organismen undergraver sine egne livsbetingelser. Den største risiko knytter sig til, at de livsopretholdende systemer ændres på måder, der gør kloden mindre egnet til at være beboet af mennesker. De livsopretholdende systemer har for eksempel betydning for atmosfærens sammensætning, vandkredsløbet, næringsstofkredsløbet, planternes bestøvning og jordens frugtbarhed. Klimaudfordringen er en af de mange udfordringer, der udspringer af, at samfundsøkonomiens metaboliske organisme er blevet for stor. Mange af udfordringerne hænger sammen, for eksempel fordi forsøgene på at begrænse brugen af fossile brændsler fører til øget brug af biomasse til energiformål og dermed til overudnyttelse af landbrugsarealerne og vandressourcerne samt pres på biodiversiteten.
[otw_shortcode_info_box border_type=”bordered” border_style=”bordered”]Grænser for Vækst
I 1972 publicerede en gruppe unge forskere på MIT i USA et banebrydende modelstudie ved navn ‘Grænser for Vækst’. I studiet brugte man en regnemodel til at lave forskellige globale scenarier for fremtiden. I scenarierne forsøgte man at fremskrive udviklingen af fem globale variable under forskellige betingelser. De fem variable var: befolkning, fødevareproduktion, industriel produktion, forurening og forbrug af ikke-fornybare ressourcer. Et af scenarierne blev kaldt ‘standardforløbet’ og var et bud på, hvordan de fem variable ville udvikle sig, hvis den globale økonomi fortsatte i sit hidtidige vækstspor. Ifølge modelberegningerne vil dette føre til et sammenbrud af den globale økonomi i midten af det 21. århundrede, hvis man ikke ændrede kurs gennem politiske indgreb. Gruppens rapport blev modtaget med udbredt skepsis og mødte meget stor modstand fra mainstreamøkonomer og politikere. Rapporten blev ofte set som en forudsigelse snarere end som den advarsel, den var tænkt som. Et efterfølgende studie fra 2008, som sammenligner det oprindelige kollapsscenarie med den faktiske udvikling siden 1972, påviser en klar sammenhæng mellem scenariet og de faktiske data, hvilket antyder, at advarslen desværre ikke blev hørt.[/otw_shortcode_info_box]
[otw_shortcode_info_box border_type=”bordered” border_style=”bordered”]Planetære grænser
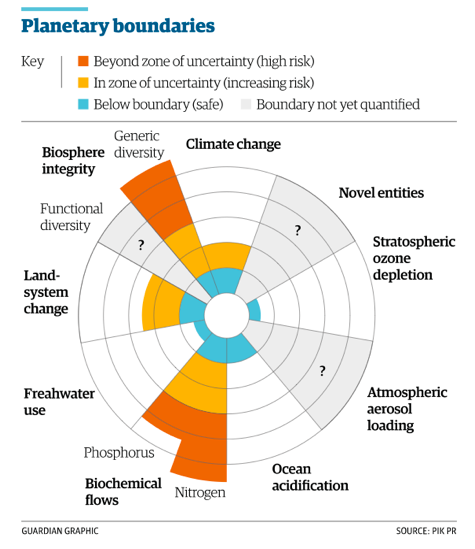
I 2009 publicerede en gruppe forskere med svenskeren Johan Rockström i spidsen et videnskabeligt studie, som har fået stor betydning for forståelsen af vores nutidige udfordringer og behovet for bæredygtig omstilling. I studiet identificerer gruppen ni såkaldte planetære grænser, som ikke bør overskrides, hvis kloden skal forblive et sikkert levested for mennesker og andre arter. Grænserne er defineret ved at undersøge menneskeligt fremkaldte, globale forandringer af en størrelsesorden, som kan betragtes som uhensigtsmæssige for klodens livsopretholdende systemer. Klimaforandringerne, tab af biodiversitet, forsuring af verdenshavene, det globale forbrug af ferskvand og konvertering af land til landbrug er nogle af de miljøproblemer, for hvilke forskerholdet har defineret planetære grænser. Med grænse menes et punkt, hvor systemet overgår til en ny tilstand. I forhold til klimaforandringerne definerer forskerne grænsen ved hjælp af mængden af CO2 i atmosfæren og anslår, at denne mængde allerede har overskredet den kritiske grænse, hvor klimasystemet er i færd med at overgå til en ny og meget mere ustabil tilstand. Flere andre planetære grænser er ifølge forskerne også allerede overskredet. Dette gælder for eksempel i tilfældet biodiversitet, hvor de mener, at tabet af arter er så langt fremskredet, at det kan få katastrofale konsekvenser for klodens økosystemer.[/otw_shortcode_info_box]
Eksponentiel vækst og fordoblingstider
De to ovenstående infobokse præsenterer to studier, som belyser et matematisk fænomen kaldet eksponentiel vækst. For at trænge lidt dybere ned i spørgsmålet om vækst og bæredygtighed er det nyttigt at beskæftige sig lidt med dette fænomen. Dette skyldes, at flere af de processer, som i øjeblikket truer vitale økosystemer og klimatiske balancer netop kan karakteriseres ved denne form for vækst.
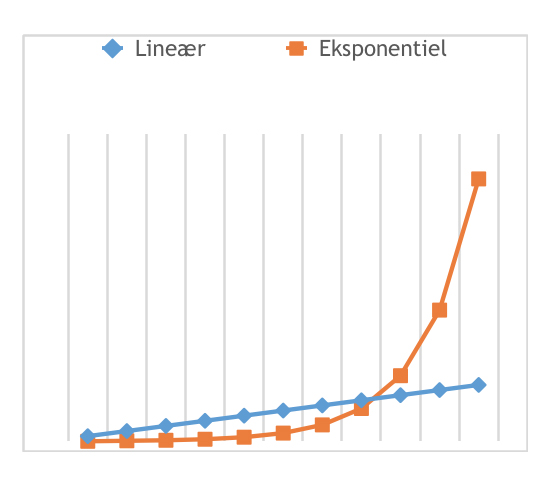
De fleste er nok bekendte med såkaldt lineær vækst, hvor noget vokser med den samme mængde for hver tidsenhed. Et barn, som vokser otte cm hvert år, eller en opsparing af lommepenge, som vokser med 10 kroner hver uge, er eksempler på lineær vækst. Eksponentiel vækst derimod er kendetegnet ved, at noget vokser med en fast procentdel af den samlede mængde for hver tidsenhed. En befolkning, som vokser med 1 % af det samlede antal om året, vokser eksponentielt. Det samme gør en opsparing, der giver en renteindtægt på 5 % om året.
Eksponentiel vækst ses blandt andet ofte i biologiske systemer. En koloni af gærceller, for eksempel, hvor hver celle deler sig i to hvert tiende minut, vokser eksponentielt med en vækstrate på 100 % pr. tiende minut. Men eksponentiel vækst findes også i økonomien, hvor BNP kan vokse eksponentielt, og i den finansielle verden, hvor ejendomspriserne for eksempel kan vokse eksponentielt og til sidst forårsage en bristende boble.
I modsætning til lineær vækst er den absolutte mængde, med hvilken en eksponentielt voksende mængde øges pr. tidsenhed, ikke konstant. Hvis man har en opsparing på 5.000.000 kr. til en rente på 5 %, så vil opsparingen det første år vokse med 250.000 kr., mens den det næste år vil vokse med 262.500 kr. og så videre. Dette forhold gør eksponentiel vækst til et drilsk fænomen, fordi væksten i begyndelsen virker tilforladelig, men pludseligt og meget hurtigt eksploderer. Dette ser vi blandt andet i det fænomen, som nogle har kaldt den store acceleration (se tema 1), hvor en lang række størrelser, som den globale befolkning og ressourceforbruget, er vokset eksponentielt og eksploderet i nyere tid. Denne vækst har lagt et stor pres på og truer nu med at nedbryde vigtige globale økosystemer.
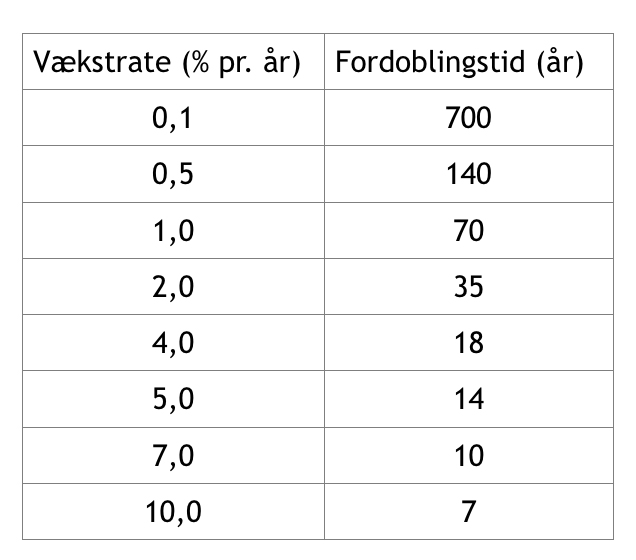
Et vigtigt begreb i forbindelse med eksponentiel vækst er fordoblingstiden, altså den tid, det tager for en bestemt mængde at blive dobbelt så stor. Der findes forskellige illustrative fortællinger om det lumske og overraskende i fordoblingstiden ved eksponentiel vækst. En gammel anekdote fortæller for eksempel, at kejseren af Kina ville belønne opfinderen af skakspillet med en gave som tak for dette fantastiske spil. Opfinderen bad nu om at få ris i gave. På første felt af skakbrættet skulle man lægge 1 riskorn, på det andet 2, på det tredje 4, på det fjerde 8 og så fremdeles. På hvert nyt felt skulle der altså lægges det dobbelte, af hvad der lå på det forrige. Det var dog et beskedent ønske, tænkte kejseren, men snart skulle det vise sig, at kejseren ikke kendte til eksponentiel vækst, for i hele det store Kina havde man ikke ris nok til at efterkomme opfinderens ønske. Det er nemlig sådan, at allerede før man når til det sidste felt i skakspillet, vil antallet af riskorn overstige den samlede globale risproduktion i dag. Og når man kommer til det sidste felt, skal der på dette felt lægges 263 riskorn, et svimlende stort tal. I tillæg til denne anekdote skal det nævnes, at væksten i hver fordoblingstid er større end al den foregående vækst. Så for hver gang mængden fordobles, skal der lægges mere til end hele mængdens tidligere vækst.
Et andet eksempel på fordoblingstid kommer fra en gammel fransk gåde om åkander, som viser, med hvilken pludselighed noget kan vokse. Gåden lyder som følger: Du ejer en lille sø, hvori der vokser en åkande. Hver dag fordobles det areal af søens overflade, som planten dækker med sine flydende blade. Hvis du ikke sørger for at holde åkandens vækst nede, vil den dække hele søen i løbet af 30 dage. Sker dette, kommer der ikke nok sollys til søen, hvilket vil være katastrofalt for de andre arter, som lever i søen. I mange dage fylder åkanden ikke alverden, så du gør ikke noget for at begrænse dens vækst. Faktisk beslutter du, at du først vil gøre noget ved åkanden, når den dækker halvdelen af søens overflade. Spørgsmålet er nu, hvilken dag det er? Svaret er dag nummer 29, altså dagen før den fylder hele søen, og da har du altså kun en dag tilbage til at gøre noget ved problemet. Moralen i denne gåde er, at eksponentiel vækst kan virke uproblematisk og overskuelig, indtil det pludselig kan være for sent at gøre noget ved problemet.
Et af de forhold, som gør vores nutid så kompliceret, er, at den er kendetegnet ved sammenfiltret eksponentiel vækst i flere forskellige variable: forbrug af ressourcer, forurening, den globale befolkning, huspriser m.m. Som vi har forsøgt at illustrere, er eksponentiel vækst et lumsk fænomen, som gør det meget svært at gennemskue udviklingen i disse sammenfiltrede variable og systemer.