Biophysical limits to growth
Emil Urhammer & Inge Røpke
One of the consequences of the biophysical perspective on the economy is the emphasis on limits to growth. In the biophysical perspective, the Earth is a system that primarily gets its energy from the sun, while the economy is seen as a metabolic organism that develops within the limits of the biosphere. The larger the organism – based on an ever-increasing flow of energy and materials – the greater the risk of the organism undermining its own conditions for life. The greatest risk is that the life-sustaining systems will be changed in ways that make the Earth less habitable for humans. The life-sustaining systems, for example, have an influence on the composition of the atmosphere, the water cycle, the nutrient cycle, the pollination of plants and soil fertility. Climate change is one of the many challenges that have arisen as a result of the fact that the economy’s metabolic organism has become too large. Many of the challenges are linked because, for example, attempts to restrict fossil fuel use lead to the increased use of biomass for energy purposes and, thus, to the overexploitation of agricultural land and water resources and pressure on biodiversity.
[otw_shortcode_info_box border_type=”bordered” border_style=”bordered”]Limits to Growth
In 1972, a group of young researchers at MIT in the United States published a groundbreaking study called ‘Limits to Growth’. In the study, a calculation model was used to prepare different global scenarios for the future. In the scenarios, an attempt was made to extrapolate the development of five global variables under different conditions. The five variables were: population, food production, industrial production, pollution and consumption of non-renewable resources. One of the scenarios was called the ‘standard run’, which was an estimate of how the five variables would change if the global economy continued on its current growth path. According to the model calculations, this would result in the collapse of the global economy in the middle of the 21st century if the course was not changed through political interventions. The group’s report was received with widespread scepticism and was met with great opposition from mainstream economists and politicians. The report was often seen as a prediction rather than as the warning it was intended to be. A subsequent study from 2008, which compares the original collapse scenario with the actual development since 1972, shows a clear connection between the scenario and the actual data, which suggests that the warning has unfortunately not been heard.[/otw_shortcode_info_box]
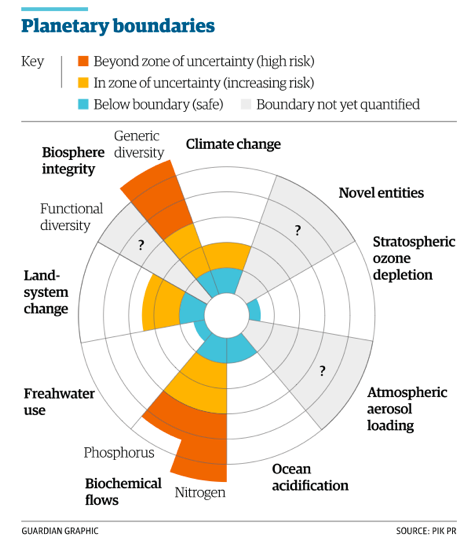
[otw_shortcode_info_box border_type=”bordered” border_style=”bordered”]Planetary boundaries
In 2009, a group of researchers led by the Swede, Johan Rockström, published a scientific study that has made a major contribution to the understanding of our present challenges and need for a sustainable transition. In the study, the group identifies nine so-called planetary boundaries, which must not be exceeded if the Earth is to remain a safe habitat for humans and other species. The boundaries were determined by investigating human- induced global changes of a magnitude that may be considered undesirable for the Earth’s life-sustaining systems. Climate change, biodiversity loss, acidification of the oceans, global consumption of fresh water and conversion of land to agriculture are some of the environmental problems for which the research team has defined planetary boundaries. By boundary is meant the point where the system transforms to a new state. With regards to climate change, the researchers determine the limit with the help of the amount of CO2 in the atmosphere and they estimate that this amount has already exceeded the critical limit at which point the climate system is about to transition to a new and much more unstable state. According to the researchers, several other planetary boundaries have also already been exceeded. This is true, for example, in the case of biodiversity as they believe that species loss is so advanced that it can have catastrophic consequences for the Earth’s ecosystems.[/otw_shortcode_info_box]
Exponential growth and doubling time
The two info-boxes above present two studies that highlight a mathematical phenomenon called exponential growth. In order to investigate the issue of growth and sustainability a little more, it is useful to focus on this phenomenon. This is because several of the processes that are currently threatening vital ecosystems and climatic balances are characterised by this kind of growth.
Most are familiar with so-called linear growth, where something grows by the same amount for each unit of time. For example, a child who grows eight centimetres a year, or a savings of pocket money that increases by 10 kroner each week. Exponential growth, on the other hand, is characterised by something that increases by a fixed percentage of the total amount for each unit of time. A population that increases by 1% of the total amount a year grows exponentially as does a savings with an interest rate of 5% per annum.
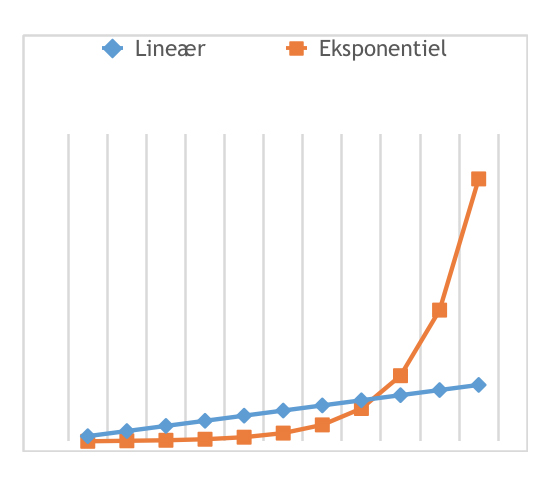
Exponential growth is often seen in biological systems. A colony of yeast cells, for example, where each cell divides in two every ten minutes grows exponentially with a growth rate of 100% every tenth minute. However, exponential growth is also found in the economy, where GDP may grow exponentially, and in the financial world where property prices can grow exponentially, which may eventually result in the bursting of a bubble.
In contrast to linear growth, the absolute amount with which an exponentially growing amount increases per time unit is not constant. If you have savings of 5,000,000 DKK at an interest rate of 5%, the savings will grow by 250,000 DKK in the first year, while in the next year, it will grow by 262,500 DKK, etc. This relationship makes exponential growth a tricky phenomenon because in the beginning, the growth seems to be harmless, but suddenly and very quickly it can explode. We can see this when we look at the phenomenon that some have called the great acceleration (see section 1), where a large number of factors, such as the global population and resource consumption, have grown exponentially and exploded in recent times. This growth has resulted in a lot of pressure and is threatening to destroy important global ecosystems.
An important concept in relation to exponential growth is doubling time, i.e. the time it takes for a certain amount of a particular unit to become twice as large. There are a number of stories that illustrate the surprising nature of doubling time in relation to exponential growth. For example, there is an ancient anecdote about the emperor of China, who wanted to reward the inventor of chess with a gift to say thank you for the amazing game. The inventor asked for a gift of rice. On the first square of the chessboard, the emperor was asked to put one grain of rice, on the second; two, on the third; four, on the fourth; eight, etc. On each new square, double the number of grains that were on the previous square. The emperor thought that this was a modest request, but he apparently was unaware of exponential growth because there was not enough rice in the whole of China to meet the inventor’s wish. Indeed, even before reaching the final square on the chessboard, the number of rice grains would exceed today’s total global rice production. And when reaching the final square, you would have to put down 263 grain of rice, which is a fantastically large number. It should be mentioned that the growth in each doubling time is greater than all the previous growth. Therefore, every time the amount doubles, more than the entire previous growth needs to be added.
Another example of doubling time comes from an old French riddle about water lilies, which illustrates how suddenly something can grow. The riddle is as follows: You own a small lake on which there grows a water lily. Every day, the area of the lake’s surface that the plant covers with its floating leaves doubles. If you do not keep the water lily’s growth in check, it will cover the entire lake in 30 days. If this happens, not enough sunlight will reach the lake, which will be catastrophic for the other species living in the lake. For many days, the water lily does not cover much of the lake, so you do nothing to limit its growth. In fact, you decide that you will only do something about it when it covers half of the lake’s surface. The question is – on which day will that be? The answer is day number 29; that is the day before it covers the entire lake, which means that you only have one day to do something about the problem. The morale of this riddle is that exponential growth may seem unproblematic and manageable, but it suddenly becomes too late to do anything about the problem.
One of the factors that make our present time so complicated is that it is characterised by interlinking exponential growth with regards to several variables: consumption of resources, pollution, global population, house prices, etc. As we have tried to illustrate, exponential growth is a tricky phenomenon which makes it very difficult to discern the change in these interlinking variables and systems.
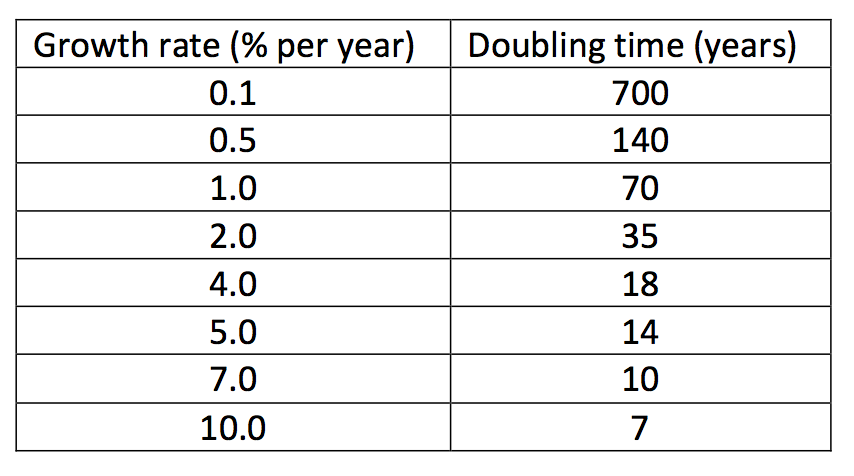
Overview of the doubling times of different growth rates. There is a rule of thumb for estimating the doubling time of exponential growth. You simply divide the number 70 by the growth rate. Example: Growth rate = 5%. 70/5 = 14.
Next: Production result – the ’real cake’